Что такое трехмерное пространство
Трехмерное пространство... Звучит как строка из фантастического рассказа... Ну очень похоже. Трехмерное пространство - это просто расширение двухмерной плоскости. Надо сразу отметить, что рендеринг трехмерной графики весьма сложен. Вообще же, сложность рендеринга экспоненциально возрастает с добавлением новых измерений и происходит это оттого, что и сами образы при этом усложняются. Наша задача заключается в том, чтобы понять, как работать с новым измерением. Мы должны все это изучить.
Говоря языком математики, любая точка в трехмерном пространстве описывается с помощью уникального набора трех координат: х, у и z. Как мы уже обсуждали ранее, обычно экран представляется плоскостью Х и Y, а координата z перпендикулярна экрану.
В отличие от плоскости, где х-координата горизонтальна, а у-координата вертикальна, трехмерные системы координат бывают двух типов:
§ Левосторонняя система координат;
§ Правосторонняя система координат.
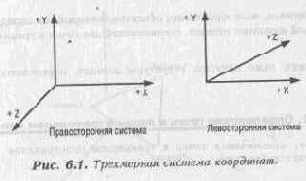
На рисунке 6.1 показано представление обоих способов отображения трехмерных систем.
В дальнейшем для всех наших рассуждений, примеров и программ мы будем использовать только правостороннюю' систему координат. На то есть две причины:
§ Правосторонняя система удобней в работе, поскольку в ней проще выполняется визуализация;
§ Правосторонняя система распространена как стандарт.
Конечно, вы можете сказать, что экран компьютера — это плоскость, и мы не можем преобразовывать трехмерные образы в двух измерениях. Верно. Вы абсолютно правы. Но у нас есть возможность отобразить их на плоскость. Мы даже можем видеть «тени» объектов. И сделать это позволит проекция. При этом модель выглядит на двухмерном экране так, что у зрителей возникает полное ощущение объемности. Такие игры как DOOM и Wolfenstein трехмерны только в нашем восприятии. Можно сказать, что в них смоделирован особый случай трехмерного пространства, образы которого можно обрабатывать гораздо проще и быстрее.
В любом случае, мы еще к этому вернемся, а теперь давайте поговорим об основных понятиях трехмерного пространства.